Two Shuffles Make a RAM: Improved Constant Overhead Zero

Two Shufﬂes Make a RAM: Improved Constant Overhead Zero Knowledge RAM

Yibin Yang

Georgia Institute of Technology

David Heath

University of Illinois Urbana-Champaign

Abstract

We optimize Zero Knowledge (ZK) proofs of statements

expressed as RAM programs over arithmetic values. Our

arithmetic-circuit-based read/write memory uses only

input

gates and

multiplication gates per memory access. This is

an almost

3×

total gate improvement over prior state of the

art (Delpech de Saint Guilhem et al., SCN’22).

We implemented our memory in the context of ZK proofs

based on vector oblivious linear evaluation (VOLE), and we

further optimized based on techniques available in the VOLE

setting. Our experiments show that (1) our total runtime im-

proves over that of the prior best VOLE-ZK RAM (Franzese

et al., CCS’21) by

2-20×

and (2) on a typical hardware setup,

we can achieve ≈ 600K RAM accesses per second.

We also develop improved read-only memory and set ZK

data structures. These are used internally in our read/write

memory and improve over prior work.

1 Introduction

Zero Knowledge (ZK) proofs [28] allow a prover

to demon-

strate to a veriﬁer

the truth of some statement while reveal-

ing nothing additional. ZK is a powerful technology with a va-

riety of applications, e.g., private blockchain [39], private bug-

bounty [32], private software analysis [25,35], ZKML [45],

private network auditability [29], and many more.

General-purpose ZK systems often express proof state-

ments as circuits or constraint systems over Boolean or arith-

metic values. However, the past decade has shown increased

interest in expressing statements as random access machine

(RAM) programs [6, 8, 10, 11, 13, 14, 20, 26, 30, 31, 33, 37, 41].

The RAM-ZK paradigm is exciting both because some state-

ments are made more efﬁcient by the random access capabil-

ity and because RAM-ZK opens the door to handling state-

ments written in commodity programming languages (see

e.g. [6, 32]). Thus, RAM-ZK promises to allow a broad audi-

ence to use widely available tools to build efﬁcient proofs of

arbitrary statements. If we hope to deliver on this promise, it

is crucial to develop RAM-ZK that is as efﬁcient as possible.

The cost of ZK proofs. General purpose ZK systems incur

three primary costs: proof size (communication),

computa-

tion, and

computation. The literature has generated many

approaches to ZK, and these approaches achieve varying lev-

els of efﬁciency with respect to these metrics.

Seeking RAM improvement for a variety of circuit-based

ZK systems, we instead focus on the total circuit size metric,

the improvement of which implies improvement to all basic

costs. Speciﬁcally, we reduce the size of circuit needed to im-

plement ZK RAM, and our results accordingly imply general

improvement to ZK RAM.

Constant overhead ZK RAM. Recently, [20] demon-

strated a reduction from ZK RAM to arithmetic circuits where

the size of the arithmetic circuit scales linearly with the num-

ber of memory accesses. I.e., the number of gates needed for

each RAM access is only a constant.

While this asymptotic scaling is ideal, the underlying con-

stants remain relatively high. In most arithmetic ZK systems,

we are most interested in reducing the number of non-linear

gates, which include multiplication gates and input gates (lin-

ear gates are typically far cheaper). The [20] construction uses

27 non-linear gates per access.

The full version of this paper is publicly available [48].

1.1 Our Contribution

We construct constant overhead ZK RAM with state-of-the-art

circuit size. Given standard arithmetic circuits, our construc-

tion uses only

input gates and

multiplication gates per

RAM access (and a constant number of linear gates).

The gates in our RAM are highly structured: viewing the

circuit globally, ﬁve of six multiplication gates are each part

of a large product computation (i.e., a high fan-in gate). This

structure is important because in some ZK systems, it is possi-

ble to exploit such structure to further improve performance.

We implemented our RAM in the context of ZK based on

vector oblivious linear evaluation (VOLE) [3

–

5, 22, 23, 44

–

47], a ZK paradigm noted for its fast end-to-end proofs (see

discussion of VOLE-based ZK in Section 2.3). We use an idea

suggested by [26] to leverage QuickSilver’s [47] support for

polynomial evaluation to take advantage of circuit structure

and signiﬁcantly decrease total cost. Our implementation is

publicly available (see the full version).

Prior work [26] developed a ZK RAM specialized for

VOLE-based techniques. We compare to their publicly avail-

able implementation [43]; our experiments (see Section 6)

show that our end-to-end proof runtime performance outper-

forms that of [26] by

2-20×

, depending on the network band-

width and the RAM size.

We also present related ZK data structures: a read-only

memory (ROM) and a set membership structure whose per-

formance substantially improves the state of the art. Our ZK

ROM outperforms that of [26] by

3-34×

, depending on the

network bandwidth and the ROM size. On a standard setup,

it can execute each access in under 1µs.

While our constructions leverage novel insights, their de-

signs are conceptually simple and easy to implement. The

results are also highly generic, and are suited to any ZK sys-

tem (even those that use, e.g., R1CS instead of circuits) with

support for (1) arithmetic gates over a large ﬁeld and (2)

public-coin random challenges. Indeed, our results are ap-

plicable to arithmetic ZK systems in the commit-and-prove

paradigm [17] (see Appendix A), including VOLE-based sys-

tems, proof systems based on MPC-in-the-head, e.g. [1,19,34],

and zkSNARKs, e.g. [2, 15, 18, 36].

1.2 Intuition

A key insight behind ZK RAM is that the ZK prover

can act

as an oracle, providing as input the correct data corresponding

to each memory access. However,

might try to cheat, on

each access providing arbitrary values that lead to an erro-

neous “proof”. The challenge is thus to check that malicious

P inputs memory values correctly.

Prior state-of-the-art ZK RAM [20, 26] build such checks

from permutation proofs (see Section 2.2), which allow

to convince the veriﬁer

that one vector of wire values is

a permutation of another. Based on this, [20, 26] allow

introduce two vectors. One vector is a list of memory access

metadata arranged in the order accesses occur in the program;

the second vector is the same metadata arranged in order

of memory address. The ﬁrst vector is used to satisfy each

memory access; the second is used to prove

did not cheat.

proves that the two vectors are related by a permutation,

then uses a circuit to scan the second vector, proving global

consistency properties of the vector.

While conceptually simple, this global check introduces

inefﬁciency in the form of large numbers of inputs from

and relatively costly comparisons (see Section 3 for details).

Our construction also leverages permutation proofs, but

its permuted vectors are (1) the list of elements written to

RAM (with metadata) and (2) the list of elements read from

RAM (with metadata). We discard [20, 26]’s global consis-

tency check in favor of a local check performed each time an

element is accessed:

Check 1. The memory element read from RAM at time

was

also written to RAM at some time t

′

, and in particular t

′

< t.

Our key insight is that – with careful design – locally per-

forming Check 1 enforces a global consistency property sufﬁ-

cient to achieve a sound protocol.

Our approach requires fewer gates than prior work because

(1) we can assemble our two vectors with fewer inputs from

and (2) our local checks can exploit static information avail-

able at the time of each access. For instance, [20, 26]’s con-

sistency check must explictly check whether two compared

addresses are equal to each other or not; for us, this check is

irrelevant, as from our permutation check we implictly know

that the read value is equal to some past write value to the

same address.

In total our entire proof uses:

•

A permutation proof (reads are a permutation of writes).

•

A per-access set membership proof (the corresponding

write was made in the past).

•

A per-access multiplication (used to multiplex the effect

of load versus store).

We give a set data structure that implements our membership

proofs and that can be achieved from a single permutation

proof. Thus, the entire RAM essentially reduces to two permu-

tation proofs (and one auxiliary multiplication). This yields a

small circuit that is fast to execute and easy to implement.

2 Preliminaries and Notation

2.1 Universal Composability

We formalize security in the universal composability (UC)

framework [16]. Our protocol is proven secure in the presence

of a malicious, static adversary. See the full version for a

review of the UC framework.

2.2 Checking Permutations via Polynomials

Our approach relies on efﬁcient permutation proofs. Namely,

given two vectors x and y stored on arithmetic circuit wires,

we wish for

to prove to

that there exists some permuta-

tion

such that x

= π(

)

. When x and y are indeed related by

a permutation, we write x ∼ y:

x ∼ y ⇐⇒ ∃π,x = π(y)

One approach to proving x

∼

y uses circuit structures called

permutation networks [9, 42]. Such networks can permute

wire values using

O(n · log n)

gates. Several works use such

networks in the context of ZK RAM [6,8,30,31]. The inherent

logn overhead is relatively expensive in practice.

A more efﬁcient approach observes that to prove x

∼

y it

is not necessary to compute a permutation

. Instead,

can

prove non-constructively that such a permutation exists with

high probability. To achieve this, prior work [38] suggested

interpreting the two vectors x and y as polynomials, and then

testing those polynomials for equality. Namely, we can view

x (resp. y) as a polynomial

(resp.

) with formal parameter

X where each element x[i] (resp. y[i]) is a polynomial root:

p(X) =

∏

(X −x[i]) q(X) =

∏

(X −y[i])

If the two vectors x and y are indeed related, then they contain

the same roots, and hence they encode the same polynomial.

Thus, to prove that x and y are related, it sufﬁces to prove that

p and q are the same polynomial:

x ∼ y ⇐⇒ p = q

Checking equality of two polynomials can be achieved with

high probability using the well known polynomial identity

test. In this test, we uniformly sample a value

r ∈ F

, and then

check if

p(r) − q(r) = 0

. The well known fact is that if this

check passes, then

and

are indeed the same polynomial

with very high probability. Speciﬁcally, if

p ̸= q

, then the

check will succeed with probability only

, where

is the

degree of the polynomial [21, 40, 51].

In the ZK setting,

can send

as a random challenge, then

and

can evaluate

p(r)

and

q(r)

via an arithmetic circuit

that grows linearly with low constants in the length of x and

y. Indeed, if x and y are length

, then the check requires only

2n − 2 multiplications (and 2n + 1 subtractions).

The above deﬁnitions of

p,q

work when x and y are vectors

of individual ﬁeld elements. However, we will need to con-

sider vectors of tuples of ﬁeld elements. [20] points out that

the above polynomial checks can be extended to vectors of

tuples by taking a random linear combination of the content

of each tuple. Suppose x and y are vectors of

ℓ

-tuples, and

let

⟨ · ⟩

denote the vector inner product operation; we can

redeﬁne p and q as follows:

p(X, Y) =

∏

(X −⟨Y · x[i]⟩) q(X ,Y) =

∏

(X −⟨Y · y[i]⟩)

Y is a length-

ℓ

vector. Thus,

and

now denote multivariate

polynomials over

ℓ + 1

arguments, but otherwise [20] proves

that the reasoning is the same.

In the ZK setting, we can check

p = q

by (1) allowing

to choose two random challenges

r ∈ F

and s

∈ F

ℓ

, (2)

computing

p(r,

)−q(r,

)

inside ZK, and (3) checking that the

result is indeed zero. Note, the challenge vector s is a public

value known to both

and

, so evaluating

p(r,

) − q(r,

)

still requires only 2n − 2 private-input multiplication gates.

2.3 VOLE-based Zero Knowledge

The literature has generated many powerful ZK proof systems

suited to various settings. Our ZK data structures are highly

generic, relying only on typical features of ZK systems for

arithmetic circuits. Still, we ﬁnd it instructive to implement

our approach in the context of a particular ZK system, and to

demonstrate clear concrete improvement.

We implement our approach in the ZK paradigm based on

vector oblivious linear evaluation (VOLE) [3

–

5,22,23,44

–

47].

VOLE-based ZK is an interactive ZK technique notable for

its linear scaling (with low constants) in all cost metrics. This

scaling makes VOLE-based ZK useful when the goal is to

complete a ZK proof as fast as possible; prior work has shown

that VOLE-based ZK can handle

≈ 5

million arithmetic mul-

tiplications per second [47].

VOLE-based ZK is particularly interesting for large, com-

plex statements, for instance those that demonstrate the exis-

tence or non-existence of software vulnerabilities in a com-

plex code-base (see e.g. [32, 35]). In the context of large,

general-purpose statements, RAM becomes a crucial ingre-

dient, as it supports programs with large data and complex

branching/looping control ﬂow.

We choose to implement in the VOLE-based ZK paradigm

because VOLE-based ZK is well suited to the complex proofs

supported by RAM. As an additional convenience, prior

work [26] is also based on VOLE, allowing a clean compari-

son. Our VOLE-based implementation builds on the publicly

available EMP Toolkit [43]. See the full version for a standard

VOLE functionality.

2.4 Miscellaneous Notation

We consider read-only and read/write memories. We use

denote the number of memory elements stored and

to denote

the number of accesses. In our analysis, we often assume there

are a large number of accesses, i.e. that

T = ω(n)

. We consider

memories that store tuples of

ℓ

ﬁeld elements. All operations

are over a prime ﬁeld

F = Z

for prime

; we require that

|F| ≥ 2T

, sufﬁcient to embed memory-speciﬁc values in the

ﬁeld without overﬂow.

We index a vector x at index

using bracket notation: x

[i]

Indexing starts at zero.

We use

∼

to denote an operation that checks its two vector

arguments are related by a permutation.

We denote logical memory operations by load and store,

and disambiguate these from physical operations read and

write. Each of our logical operations requires one read and one

write. Our circuits use constants load = 0 and store = 1.

We refer to the ZK prover

by she/her/hers and to the ZK

veriﬁer V by he/him/his.

We refer to ZK operations that multiply two private val-

ues or require

to provide input as non-linear. Operations

that add two private values, subtract two private values, or

input

ℓ

: 1 → F

ℓ

∼ : (F

ℓ

)

× (F

ℓ

)

→ 1

0,1,2,... : F

+ : F × F → F

− : F × F → F

· : F × F → F

Figure 1: Syntax on which we build our RAM. We consider

circuits over a ﬁeld

with support for permutation checks.

We include gates that accept

ℓ

inputs from

, gates that check

two vectors of

ℓ

-tuples are related by a permutation, gates

that add/subtract/multiply wires, and wires that hold constants.

Section 2.2 discusses how ∼ can be implemented.

input

ℓ

: 1 → F

ℓ

0,1,2,... : F

make-mem : (F

ℓ

)

→ mem-id

+ : F × F → F

− : F × F → F

· : F × F → F

access : mem-id × F × F × F

ℓ

→ F

ℓ

Figure 2: Our target syntax supports arithmetic gates and

gates that manipulate random access memories.

make-mem

generates a fresh memory and

access

loads/stores to a mem-

ory. Figure 4 speciﬁes semantics.

scale a private value by a public value are linear. Typically,

non-linear operations are far more expensive than linear oper-

ations. Accordingly, our cost accounting precisely enumerates

only the number of non-linear operations.

2.5 Models

Our goal is to UC-realize the functionality

ram

(Figure 4).

This functionality allows arbitrary arithmetic circuits aug-

mented with random access memory. We achieve this func-

tionality given access to circuits with arithmetic gates and

support for permutation proofs (Figures 1 and 3). As discussed

in Section 2.2, such permutation proofs can be achieved from

standard arithmetic circuits with support for public coin ran-

dom challenges, so our approach can be implemented on top

of standard arithmetic ZK techniques.

Our functionality

ram

can serve as the basis for arbitrary

ZK CPU architectures, as have been explored by prior work,

e.g. [6, 26, 32, 49].

Boolean vs. arithmetic circuits. We develop ZK RAM

compatible with arithmetic gates. It is well known that

Boolean and arithmetic circuits trade off in efﬁciency. For in-

stance, arithmetic circuits are better at multiplication; Boolean

circuits are better at comparisons.

We believe that in the ZK setting and for large proofs, it is

becoming clear that arithmetic circuits are a superior model

of computation. Indeed, the introduction of fast arithmetic-

Functionality F

perm

Let

be an arithmetic circuit with permutation check gates

(i.e.,

is written in the syntax of Figure 1).

perm

in-

teracts with

, and the adversary

. Upon receiving

(prove,C,w) from P and (verify,C) from V :

•

If when running

)

it holds that (1) the circuit out-

puts

and (2) for each internal call to x

∼

y, x and

y are indeed related by a permutation, then output

(C,true)

and

; else output

(C,false)

and V .

Figure 3: The functionality for Zero Knowledge proofs over

arithmetic circuits with access to a permutation check gate.

Figure 1 deﬁnes syntax of such circuits.

circuit-based read-only memory (ROM) – such as the state-

of-the-art ROM introduced in this work – can signiﬁcantly

mitigate the downside of arithmetic circuits.

As an example, consider the problem of comparing two,

say,

-bit values. This problem can be solved by subtracting

the one value from the other and then looking up the differ-

ence in a ROM with

entries. For negative indices, the

ROM stores a

; for positive indices it stores a

. To compare

larger numbers, we can ﬁrst break the numbers into chunks,

element-wise compare chunks, and combine the results. As

long as enough comparisons are performed across the proof,

this approach yields comparison operations for only a small

constant number of arithmetic gates.

3 Related Work

Approach of Franzese et al. [26]. [26] constructed the ﬁrst

concretely efﬁcient ZK RAM with constant overhead. Their

approach works in the VOLE-based ZK setting for mixed

circuits containing both arithmetic and Boolean gates

. [26]

leverages permutation proofs (Section 2.2). We compare our

performance to that of [26] in Section 6.

The [26] approach is as follows. On each memory access

to address

addr

provides the loaded value

val

as part of her

input. Then, the system records a

-tuple of (1) the address

addr

, (2) the time

of the access (according to a monotonically

increasing clock), (3) a bit

indicating if this access is a

load

or a

store

, and (4) the value

val

that is loaded or stored.

Of course, on any particular load,

might cheat and pro-

vide an incorrect value. Hence, after all

accesses are com-

pleted, [26] performs a global consistency check. Note that

after T accesses, the system holds a vector of T 4-tuples.

In the ﬁrst step of the consistency check,

inputs a new

version of this length-

vector, where this second version

[26] targets Boolean computation, but they must pack Boolean values

into a larger ﬁeld to achieve efﬁcient permutation proofs.

Functionality F

ram

Let

be an arithmetic circuit with RAMs (i.e.,

is written

in the syntax of Figure 2).

ram

interacts with

, and

the adversary

. Upon receiving

(prove,C,

)

from

and

(verify,C) from V , execute C(w):

• For each arithmetic gate, run the gate normally.

•

For each

make-mem

gate with input vector x, store x as

a memory, initialize a fresh memory identiﬁer, asso-

ciate the identiﬁer with the stored memory, and place

the identiﬁer on the gate output wire.

•

For each

access

gate with

(id,op, addr,w)

, look up

the memory associated with

, read address

addr

, and

save the result on the gate output wire. If

op = store

then write w to memory address addr.

If the circuit output wire holds

, then output

(C,true)

S and V ; else output (C,false) to S and V .

Figure 4: Our target functionality

ram

supports arithmetic

circuits with random access memories. We achieve this func-

tionality in the F

perm

(Figure 3) hybrid model.

is sorted ﬁrst by memory address, then by time. Thus, the

accesses are grouped into memory addresses such that one

can locally scan from left to right, checking consistency.

proves that this second vector is indeed a permutation of the

ﬁrst via techniques discussed in Section 2.2.

The consistency check scans the second vector from left to

right, ensuring that (1) the vector is indeed sorted correctly

and (2) each load operation reads a value consistent with the

most recent store to the same memory address. In particular,

for each index i, [26] checks:

((addr

< addr

i+1

) ∨ ((addr

= addr

i+1

) ∧ (t

< t

i+1

)))

∧ ((addr

̸= addr

i+1

) ∨ (val

= val

i+1

) ∨ (op

i+1

= store))

∧ ((addr

= addr

i+1

) ∨ (op

i+1

= store))

With this done,

is conﬁdent that values provided by

are

correct, so the approach achieves ZK RAM.

There are several efﬁciency problems in this approach.

First, the above consistency check requires circuits that com-

pare addresses/values. A comparator on length-

ℓ

values re-

quires

Θ(ℓ)

gates, and RAM addresses/values have size

Θ(logT ). Hence, the number of gates is super-constant.

While [26] are still able to claim constant ZK commu-

nication overhead

, the super-constant number of gates is

problematic. In particular, the technique is a poor ﬁt for arith-

metic circuits, because we must simulate each Boolean gate

The [26] notion of ‘overhead’ is the total communication cost divided by

the number of bits read from RAM. Since the number of gates grows linearly

in the size of RAM words, [26] can claim constant overhead.

with arithmetic gates, incurring unacceptable cost. Many ZK

systems are best suited to arithmetic circuits, so RAM over

arithmetic values is arguably preferable.

Moreover, even [26]’s own performance suffers from the

large number of gates, not in communication, but in computa-

tion. Speciﬁcally, each of [26]’s AND gate operations requires

only

≈ 1

bit of communication, but it also requires that both

and

perform operations over the ﬁeld

where

is a

computational security parameter (e.g.

128

). Together, these

operations are expensive.

In our approach, we construct arithmetic ZK RAM where

the total number of gates is a small constant. This allows

us to build VOLE-based ZK where all costs have constant

overhead, allowing us to signiﬁcantly improve over [26] in

terms of total wall-clock time performance. Indeed, while we

achieve only a small communication improvement over [26],

we improve in wall-clock time by up to 20×.

Approach of Delpech de Saint Guilhem et al. [20]. [20]

were the ﬁrst to achieve ZK RAM whose arithmetic circuit

size is linear in the number of RAM accesses

. Hence, unlike

[26], [20] achieves constant overhead in all costs.

In short, [20] leverages the same approach as [26], except

that they carefully optimize the comparison/equality opera-

tions. [20]’s key ingredient is an elegant bounds check, and

this check is used to implement comparison.

The [20]’s bounds check proceeds as follows. Suppose

the arithmetic circuit holds a length-

vector x

∈ F

, and

would like prove in batch that each element of x is in

1,...,T

To achieve this, [20] ﬁrst constructs the following vector:

y = x[0],x[1],...,x[T − 2],x[T − 1], 1, 2, 3, ..., T − 1,T

[20] then requires that

inputs a new vector z and proves

that z is a permutation of y: y

∼

z. If

is honest, then she will

input z in sorted order. With this done,

can prove that all

elements x

[i]

are in the range

1,...,T

by proving that (1) the

last element of z is

and (2) the difference between any two

consecutive elements z

[i + 1] −

[i]

is either

. It is easy

to perform this check with a linear-size arithmetic circuit.

[20] uses this linear-sized circuit to handle all comparisons

of the [26] consistency check in batch. Equality computations

can similarly be handled by a constant overhead circuit. Thus,

[20] removes the logarithmically-sized circuit components

from [26], achieving true constant overhead in circuit size.

While [20] indeed improves over [26], it retains inefﬁcien-

cies of [26]’s consistency check, so the approach still requires

27 non-linear gates per access.

[20] specialized their approach for the ZK paradigm based

on ‘MPC-in-the-head’ [19,34], but since it is an arithmetic cir-

cuit, it can be used in other paradigms as well. Indeed, we im-

plemented [20]’s approach in the VOLE-based ZK paradigm

so that we can compare to it (see Section 6).

Our ZK RAM leverages a fundamentally different approach

to consistency, allowing us to achieve RAM from fewer gates.

Other related work. A number of other works [7, 8, 30

–

32, 41] achieved proof system RAM. These works are based

on permutation networks [9, 42], requiring polylogarithmic

overhead for each access.

[13] was the ﬁrst to achieve only super-constant prover

cost based on shufﬂe proofs, e.g. [38]. Their approach is not

practical, as explicitly stated by the authors.

[14] developed proofs for programs in the Map-Reduce

model; they do not achieve general RAM.

We note that our ZK ROM shares some similarities with

Plonk’s lookup table literature (starting from [27]). Similar in-

tuition to our ZK RAM has been applied in the memory check-

ing literature (e.g., [12,24, 50]), which focuses on providing a

correct outsourced memory (without ZK). Our work ensures

memory-checker-like techniques are efﬁciently handled in the

ZK setting, where we are strictly limited in that all operations

must be handled by black-box ﬁeld arithmetic. Achieving this

efﬁciently requires careful handling of ROM/RAM.

4 Technical Overview

4.1 Read-Only Memory

To begin, let us elide writes, and suppose that we wish to

implement read-only memory (ROM). Namely,

and

agree on a length-

vector of wires x, and we encode x as a

ROM data structure. Now, given an address wire

, the circuit

can query

lookup(i)

, which returns a wire holding x

[i]

. We

present an efﬁcient instantiation of lookup.

As a ﬁrst insight, observe that each call to

lookup

can

leverage honest

as an oracle; honest

knows the cleartext

value of x and

, and hence she can simply provide x

[i]

input. Of course,

might be cheating, so we must check that

each such input is indeed correct.

Our ROM data structure handles all such checks in batch by

maintaining two vectors of tuples,

reads

and

writes

. On each

call to

lookup

, we append one element to

reads

and one to

writes

. Our key insight is that with minimal added metadata,

we can ensure that each call to

lookup

is correct if and only

if reads is a permutation of writes.

Each element of

reads

(resp.

writes

) is a three-tuple of (1)

the element’s address, (2) the element’s value, and (3) a meta-

data value called the version. Versions act as address-speciﬁc

counters, and each call to lookup increments a version.

To set up our ROM data structure, for each address

i ∈ [n]

we append to writes the following tuple:

(i,x[i],0)

I.e., we initialize each element with version

. Then, on each

call to

lookup(i)

provides two inputs: (1) the value x

[i]

and (2) the latest version

associated with address

. We then

update both

reads

and

writes

by appending the old version

(i,x[i],v) to reads and a fresh version (i,x[i],v + 1) to writes.

address

time

teardown

Figure 5: Access pattern for a size-

ROM with lookup pat-

tern

2,1,2,3

. On each lookup, we read an element and write

back a fresh version of that same element. Nodes represent

writes; edges represent reads. Because (1) versions monotoni-

cally increase and (2) reads must be a permutation of writes,

even malicious

cannot read an element that was not written

at setup time. It is possible for malicious

to read elements

written “in the future” (e.g.,

can construct the graph for

address 2), but it is not possible for P to form a cycle.

When we are ﬁnished with ROM, we perform a simple

cleanup step that we call a teardown. For each address

i ∈ [n]

honest

inputs the latest version

, and we append

(i,

[i],v)

reads

. Finally,

demonstrates that the reads and writes are

related by a permutation:

reads ∼ writes

. Perhaps surprisingly,

this simple approach is already correct and sound.

Correctness. Correctness of our ROM follows from the

following key invariant:

Invariant 1 (ROM Invariant). On each call to

lookup

and

for each address

, the vector

writes

contains (at least) one

tuple of the form (i,val,v) that does not appear in reads.

The setup phase establishes Invariant 1, because it writes

version

of each element. Then, on each call to

lookup

, hon-

est

propagates Invariant 1 by reading the latest version

[i]

, and writing back a fresh version

v + 1

. Finally, the tear-

down phase reads the last version of each element, ensuring

that every written version is also read. Hence, if

is honest,

reads is indeed a permutation of writes.

Soundness. The key insight behind the soundness of our

ROM is that even a malicious

must read each version of an

element that is written, or else

reads

will not be a permutation

writes

. Moreover, on each call to

lookup

, the circuit struc-

ture ensures that for whatever version

v P

chooses to read, a

fresh version v + 1 is written.

The above two facts bind

into building per-element

chains of reads and writes (see Figure 5), where (1) each

read is made to a version written at some different point in

time, (2) the initial link of the chain is written at setup, and (3)

the ﬁnal link is read at teardown. Because each element x

[i]

written at setup is stored on circuit wires (i.e., is not a prover

input), and because on each

lookup

we write back the same

element that was read, it must be the case that all reads made

to the same address i match the initial value x[i].

Interestingly, our ROM does allow malicious

to “read

from the future”. Namely, on a particular call to

lookup(i)

malicious

can read a version of x

[i]

that is only written at

a later call to

lookup(i)

. This remains sound because the

value x

[i]

does not change over the lifetime of the ROM. The

crucial point is that it is not possible for

to form cycles,

where two calls to

lookup

each read a version written by the

other call. It is impossible to convincingly construct such a

cycle because versions monotonically increases on each call

lookup

, so

cannot arrange two versions such that each

version is greater than the other.

The ability for malicious

to read from the future is the

key distinction between ROM and full-ﬂedged read/write

RAM: in full RAM we must ensure that each of

’s read

values comes from the past.

Remark 1 (Looking up an illegal address). If a circuit calls

lookup(i)

where

is not written at setup, then the proof will

fail. This is because

cannot construct a chain, as there is

no ﬁrst link written at setup. This fact will be useful later.

Generalizing to tuples. So far, the ROM stores individual

wire values. It is easy to generalize the ROM such that each

address stores an

ℓ

-tuple of wires for arbitrary

ℓ

. This simply

requires changing the number of inputs provided by P .

Generalizing to read-only key-value stores. So far, our

ROM stores elements at addresses

0,1,...,n − 1

. It is easy

to generalize to a key-value store where the key space is an

arbitrary set. In particular, at setup we initialize the key-value

store from a list of pairs

(i,

[i])

. So long as each address

unique, this generalization incurs no extra cost. This is useful

when using key-value stores to encode sets (Section 4.2)

Gate cost. Consider a ROM of size

where

lookup

called

times. For a ROM storing

ℓ

-tuples, where

ℓ

is an

arbitrary constant, each call to

lookup

requires

ℓ + 1

inputs

from

(the

ℓ

entries of the tuple and the version), for a total of

T · (ℓ + 1)

input gates. The teardown phase similarly requires

that

reads each of the

slots, requiring

n ·(ℓ + 1)

additional

input gates. Finally, the permutation proof

reads ∼ writes

inspects vectors of length

n + T

; this can be implemented

using two fan-in

n + T

multiplication gates (see Section 2.2).

In sum, the full construction requires:

• (n + T )(ℓ + 1) input gates.

• Two fan-in n + T multiplication gates.

• O(n + T ) linear gates.

4.2 Sets with Membership Queries

As mentioned in Section 4.1, the key difference between ROM

and full-ﬂedged RAM is that in RAM we must check that

each read value was written at some time in the past. As we

will see, we achieve this by checking that on each access a

particular timing value is in a public set

{1,...,T }

, where

is the total number of RAM accesses.

We observe that our read-only key-value store (RO-KVS,

Section 4.1) is well suited to this set membership proof. In

particular, consider an RO-KVS where we set the size of

tuples to

ℓ = 0

. We initialize an RO-KVS with addresses

1,...,T

. Then, to check that a particular value

is a member

of a set, we call

lookup(t)

. This call does not return any data,

but if

is not in the set

{1,...,T }

, then the proof will fail, as

was observed in Remark 1. Thus this call to

lookup

serves

as a proof that t is in the set.

Gate cost. The cost of our set structure is inherited from

the cost of ROM. For a set with

values and

membership

queries (these parameters are used in our RAM), total cost is:

• 2T input gates.

• Two fan-in 2T multiplication gates.

• O(T ) linear gates.

4.3 Read/Write Memory

Consider a random access memory (RAM) equipped with a

single

access

instruction. Each call to

access

accepts as

input three arguments:

• op ∈ {0,1} is 0 on a load and 1 on a store.

• i ∈ F is an address.

• w

is the value to store, if this operation is indeed a store.

Each RAM access both reads and writes data, whether the

operation is a load or a store. On a store, we read the old data

and write the new data; on a load, we read the old data and

write back a fresh copy of the same data. Just like our ROM,

our RAM maintains two vectors

reads

and

writes

, and on each

access we update each vector. Also like our ROM, our RAM

checks that reads are a permutation of writes:

reads ∼ writes

As mentioned in Section 4.1, the main challenge in RAM as

compared to ROM is that we must prevent malicious

from

reading a value written in the future. Our approach here is to

maintain a monotonically increasing public value

clock

which

is set to 0 at setup and then incremented on each access.

When we write a value

val

to address

, we append the

following tuple to writes:

(i,val,clock)

address

time

teardown

Figure 6: Zero-initialized RAM with history

(store,2,13)

(store,1,42)

(load,2, )

(store,3,27)

(store,2,8)

Each node represents a write; each edge represents a read.

Our construction forces

to prove that (1) each node has one

incoming edge and (2) each edge points to the left. Point (1)

is achieved by checking that reads and writes are related by a

permutation; point (2) is achieved by a set membership proof.

This forces

to organize each address’s history as a linked

list. E.g., on operation

(store,2,8)

must read from the

immediately preceding address 2 write.

I.e., we mark each write with the time it occurred. To read

a value and ensure

reads ∼ writes

, we must also mark each

read value with the time at which that value was written.

Accordingly, each call to

access

at address

requests that

inputs two values: (1) the value

val

that was last written to

address i and (2) the time t when the write occurred.

Of course,

might be malicious, so we must check that

the input

(val,t)

is consistent with the semantics of read/write

RAM. The permutation proof

reads ∼ writes

ensures that

each such triple

(i,val,t)

is indeed written at some point in

time. The remaining challenge is to ensure that this point in

time is in the past, which can be achieved by checking that

clock − t

is a strictly positive value. Said another way, we can

check that

clock − t

is in the set

{1,...,T }

, where

is the

total number of RAM accesses. Each such check is achieved

by our set data structure (Section 4.2).

This simple set membership proof is sufﬁcient, and we do

not need to explicitly prove that each read corresponds to the

most recent write. Indeed, this stronger property (each read

comes from the latest write) is implied by the local checks

combined with the permutation proof reads ∼ writes.

To see that this is true, observe that our RAM maintains

the following key invariant:

Invariant 2 (RAM Invariant). Before each call to

access

and for each address

writes

contains exactly one tuple of

the form

(i,val,t)

that does not appear in

reads

. Moreover,

the value

is highest amongst all such tuples in

writes

; i.e.,

this tuple records the most recent write to address i.

When we set up RAM with initial content x, we append the

following write for each address

(i,

[i],0)

. Since we write

each address once, our setup trivially establishes Invariant 2.

On each call to

access

is forced to input values

(val,t)

such that

clock − t

is positive. By Invariant 2 there is only

one such choice that will pass the permutation proof, and

this choice must be the most recent version of address

, so

this access is sound. Moreover, this access propagates the

invariant because we increment the clock and write a fresh

copy of address i; see also Figure 6.

Once all

accesses are complete, note that we have written

n + T

values, but we have only read

values. We allow

complete the read history in a teardown step, where we read

(without writing back) each RAM address. In particular, for

each address

again inputs a pair

(val,t)

, and we append

(i,val,t)

reads

. Note that on this step and by Invariant 2,

we do not need to check that

clock −t

is positive; it must be,

or else the permutation proof will fail.

Generalizing to tuples. As in our ROM, it is straightfor-

ward to generalize the RAM such that each address stores an

ℓ

-tuple of wires for arbitrary constant

ℓ

. This simply requires

changing the number of inputs provided by P .

Gate cost. Our RAM has four relevant costs:

•

We maintain the set

{1,...,T }

(Section 4.2) and perform

one membership proof per access.

•

We use a permutation proof (Section 2.2) on two length-

(T + n) vectors: reads ∼ writes.

• P

inputs two values

(val,t)

on each of the

accesses,

and for each of n addresses at teardown.

•

We include a single multiplexer that disambiguates load

operations from store operations. In particular, after read-

ing old from RAM, we compute:

new ← old + op · (w − old)

If the operation type is public, this is not needed. For

completeness, we assume operation types are private.

In total, the RAM incurs the following gate cost:

• 4T + 2n input gates.

•

Two fan-in

multiplications (from the set) and two fan-

T + n

multiplications (from the permutation proof).

We optimize one of the fan-in

multiplications to be

only fan-in T ; see Section 5.2.

• T fan-in two multiplications (from multiplexers).

• O(n + T ) miscellaneous linear operations.

When we assume that the number of accesses

is signiﬁ-

cantly greater than the RAM size

, we obtain the per-access

costs listed in our contribution.

5 Approach

5.1 Formal Protocol and Security

We formalize our ZK RAM as a protocol in the

perm

-hybrid

model. This protocol formalizes ideas explained in Section 4.

Our protocol is deﬁned with respect to Figures 7 to 9.

Protocol 1.

and

agree on an arithmetic circuit with RAM

access

; i.e.,

is written in the syntax of Figure 2.

holds

as input a witness w.

and

compile

to an arithmetic

circuit with permutations (Figure 1) in the following manner:

•

For each

input

gate, addition gate, subtraction gate,

multiplication gate, and constant wire, they trivially com-

pile the circuit element.

•

For each

make-mem

gate, the parties invoke

setup

(Fig-

ure 9) which produces a circuit-based RAM data struc-

ture.

locally maintains a cleartext copy of this RAM

(and its internal set structure), allowing

to track which

value is stored at each address.

•

For each

access

gate, the parties invoke the

access

procedure of Figure 9.

extends her witness w by using

her local copy of the RAM to recall the last time

when

the queried address was accessed and what value

val

was stored there (and to ﬁnd the set version of

clock −t

)

so that these values can be passed to

input

gates.

updates her local copy of RAM.

•

Once all gates are compiled, the parties invoke

teardown

on each RAM data structure created by a

call to

setup

uses her local copy of RAM (and its

internal set) to appropriately extend her witness w.

and

thus agree on a circuit

′

with arithmetic gates

and permutation proofs. Next, (1)

sends

(prove,C

′

)

perm

, (2)

sends

(verify,C

′

)

perm

, (3)

outputs

⊥

and (4) V outputs whatever he receives from F

perm

Our key security property is that Protocol 1 achieves the

Figure 4 functionality, allowing us to securely implement ZK

proofs with RAM.

Theorem 1. Protocol 1 UC-realizes

ram

(Figures 2 and 4)

in the

perm

-hybrid model (Figures 1 and 3) with no sound-

ness error.

The full version includes a detailed proof of Theorem 1.

For now, we sketch the argument, focusing on soundness.

Proof Sketch. By construction of a simulator S.

Our protocol can be viewed as a circuit compiler that maps

arithmetic circuits with RAM (Figures 2 and 4) to arithmetic

circuits with permutations (Figures 1 and 3). Accordingly,

’s only task is to tediously convert between RAM circuits

and permutation circuits, and to collect

’s witness w before

sending it to the F

ram

functionality.

However, we still must demonstrate that

is a valid sim-

ulator, and that the UC environment cannot distinguish the

simulation from the real world protocol. The challenge in

showing this is that our compilation generates non-trivial

input

gates, allowing

extra degrees of freedom in choos-

ing a convincing witness. Therefore, we must argue that our

construction is sound. All compiled gates in Figure 2 are

trivially sound, save for make-mem and access gates.

In short, these gates are sound because our RAM construc-

tion includes a permutation proof on its reads and writes, and

because on each access we check that

’s chosen time

is less

than

clock

(this latter property is checked by a set membership

proof). As per discussion near Invariant 2, these local checks

enforce a global ordering of reads/writes on each address, on

each access forcing

to input the most recent value written

to the same address.

It remains to show that the underlying set data structure

is sound. As discussed in Section 4.1, our set (as inherited

from our ROM) on each access forces

to input a version.

Because we monotonically increase versions and because we

use a permutation proof on set reads/writes, we force

construct a linked list of read/write pairs, connecting each

read value to the setup-time write on the same address.

Together, this means that

’s extra inputs must respect the

semantics of access gates, so the protocol is sound.

Prior work on VOLE-based ZK gave powerful constant

round protocols for proving arithmetic statements. Such prior

works, together with the permutation proof method discussed

in Section 2.2 and an optimization discussed in Section 5.2,

imply the following (see Appendix B.2 for more details):

Lemma 1. There exists a

-round protocol in the VOLE-

hybrid model that UC-realizes

perm

. For each use of

input

and of

and

use

VOLE correlation; for each use of

∼

on two length-

vectors,

and

each evaluate a lin-

ear number of ﬁeld operations and consume

ε−1

+o(1)

VOLE

correlations, for any constant

ε ≥ 2

. The protocol achieves

soundness error

n+m

|F|

)

, where

is the size of the largest

vector passed to

∼

and

is the number of multiplications.

Together, Theorem 1 and Lemma 1 allow us to instantiate

ZK RAM from VOLE-based ZK:

Corollary 1 (RAM from VOLE). There exists a

-round

protocol in the VOLE-hybrid model that UC-realizes

ram

For each call to

access

on a size-

memory that is accessed

T = ω(n)

times,

and

each evaluate a constant number of

ﬁeld operations and consume

5 +

ε−1

+ o(1)

VOLE correla-

tions, for any constant

ε ≥ 2

. The protocol achieves soundness

error

T +m

|F|

)

, where

is the largest number of accesses used

by any memory and m is the number of multiplications.

1 type ro-kvs

ℓ

{

2 content : (F,F

ℓ

)

∗

3 reads : ro-kvs-record

∗

ℓ

4 writes : ro-kvs-record

∗

ℓ

5 }

1 type ro-kvs-record

ℓ

{

2 key : F

3 value : F

ℓ

4 version : F

5 }

1 lookup(m : ro-kvs

ℓ

,key : F) → F

ℓ

{

2 val ← input

ℓ

( )

3 version ← input

( )

4 m.reads.append({ key,val,version })

5 m.writes.append({ key,val, version + 1 })

6 return val

7 }

1 setup-ro-kvs

ℓ

(content : (F, F

ℓ

)

∗

) → ro-kvs

ℓ

{

2 m ← ro-kvs

ℓ

{ content, { }, { } }

3 for (key,val) ∈ content {

4 m.writes.append({ key,val,0 })

5 }

6 return m

7 }

1 teardown-ro-kvs(m : ro-kvs

ℓ

) {

2 for (key,val) ∈ content {

3 version ← input

( )

4 m.reads.append({ key,val,version })

5 }

6 m.reads ∼ m.writes

7 }

Figure 7: Our ZK read-only key-value store holds ℓ-word values at each key. We highlight uses of non-linear gates.

1 type set ::= ro-kvs

1 setup-set(content : F

∗

) → set {

2 return setup-ro-kvs

(content)

3 }

1 teardown-set(s : set) {

2 teardown-ro-kvs(s)

3 }

1 prove-member(s : set,val : F) {

2 lookup(s, val)

3 }

Figure 8: Our ZK set data structure is a specialization of our read-only key-value store (Figure 7) where each key holds

words.

An element is considered a member of the set if it is a key in the key-value store. We highlight uses of non-linear gates.

Formalizing ROM (including our set data structure). For

simplicity and because RAM is more interesting than ROM,

we chose to not formalize ROM as part of our top level func-

tionality (Figure 4). Such a formalism can be derived from our

RAM formalism by substituting RAM-related gates to initial-

ize ROM and access ROM, and correspondingly modifying

Protocol 1 according to Figure 7. Soundness of ROM gates fol-

lows from our proof of Theorem 1. We include security games

crucial for the soundness proof of ROM in Appendix B.1.

5.2 Optimizations

Accelerating permutation proofs. The main cost of our

protocol comes from permutation proofs, and permutation

proofs can be achieved by high fan-in multiplications (Sec-

tion 2.2). We note two important available optimizations.

The ﬁrst optimization is generally applicable for any ZK

system and saves

multiplications. Consider the permuta-

tion proof performed on the publicly known set

{1,...,T }

(Section 4.2). Here, the ﬁrst

writes are publicly known to be

(1,0),(2,0),...,(T − 1, 0),(T,0)

. Hence, in the permutation

proof, once

chooses a random challenge,

and

can lo-

cally compute the product of the ﬁrst

components of

writes

Again, this saves T ZK multiplications.

The second optimization leverages a VOLE-speciﬁc trick

to reduce cost of high fan-in multiplications. QuickSilver [47]

supports polynomial proofs. Namely, [47] can efﬁciently

prove a batch sub-statements of the following form:

p(x

) = 0,..., p(x

n−1

) = 0

Here,

is a degree-

polynomial over arithmetic wires. The

batch of

sub-statements requires only

VOLE correlations

(VOLE correlations are the primary cost in VOLE-based ZK).

This trick reduces VOLE correlations, but can increase com-

1 type RAM

ℓ

{

2 reads : record

∗

ℓ

3 writes : record

∗

ℓ

4 valid-diffs : set

5 clock : F

6 size : N

7 }

1 type record

ℓ

{

2 address : F

3 value : F

ℓ

4 time : F

5 }

1 setup

ℓ

(T : N,content : (F

ℓ

)

∗

) → RAM

ℓ

{

2 n ← |content|

3 valid-diffs ← setup-set(1, . . . , T )

4 m ← RAM

ℓ

{ { },{ },valid-diffs,1,n }

5 for i ∈ [n] {

6 m.writes.append({ addr,content[i],0})

7 }

8 return m

9 }

1 access(m : RAM

ℓ

,op : F,addr : F,w : F

ℓ

) → F

ℓ

{

2 old ← input

ℓ

( )

3 t ← input

( )

4 prove-member(m.valid-diffs,m.clock − t)

5 new ← old + op · (w − old)

6 m.reads.append({ addr,old,t })

7 m.writes.append({ addr,new,m.clock })

8 m.clock ← m.clock + 1

9 return old

10 }

1 teardown(m : RAM

ℓ

) → (F

ℓ

)

∗

{

2 content ← { }

3 for addr ∈ [m.size] {

4 val ← input

ℓ

( )

5 t ← input

( )

6 m.reads.append({ addr,val,t })

7 content.append(val)

8 }

9 m.reads ∼ m.writes

10 teardown-set(m.valid-diffs)

11 return content

12 }

Figure 9: Our ZK read/write memory. Each memory slot holds an

ℓ

-tuple of ﬁeld elements. The memory is deﬁned in terms of

our

set

data structure (Figure 8). We deﬁne three procedures:

setup

access

, and

teardown

. Valid usage consists of one call

setup

, an arbitrary (polynomial) number of calls to

access

, and one call to

teardown

. We highlight uses of non-linear gates.

putation, as P ’s compute scales with O(d

Polynomial proofs can optimize fan-in-

multiplications as

follows. Consider a fan-in-

multiplication for any constant

ε ≥ 2

. We can implement such a multiplication by allowing

to input a value

prod

, and then deﬁning a degree-

polynomial

that multiplies the

values and subtracts

prod

. This is a degree

polynomial, and we can use [47] to prove it equals zero

(if it does,

input

prod

correctly). It is straightforward to

use

⌈

ε−1

⌉

fan-in-

multiplications to implement a fan-in-

multiplication, so we can use

⌈

ε−1

⌉

polynomial proofs to

implement a fan-in-n multiplication.

Prior work [26] also used this trick, but their corresponding

improvement was limited, as their cost is dominated by com-

parisons, not by permutation proofs. In our approach, almost

all multiplication cost comes from high fan-in multiplications,

so we enjoy substantial improvement.

By choosing arbitrary constant

ε ≥ 2

, we reduce the number

of VOLE correlations from

≈ 10T

≈ (5 +

ε−1

. This

reduces the communication used by

and

, and it also

reduces the amount of computation needed to construct the

correlations. However, as stated above,

’s proof computation

increases as we increase

, so we limit

to constant values to

avoid asymptotic problems. In Section 6 we ﬁnd it is best to

set ε between 8 and 32, depending on the network.

To our knowledge, this polynomial proof optimization is

currently speciﬁc to VOLE-based ZK. It is possible similar

optimizations will emerge in other ZK paradigms, particularly

because ZK RAM provides compelling motivation.

Other optimizations. We discuss some additional (unim-

plemented) optimizations in the full version.

6 Evaluation

Our implementation. We implemented our ROM, our set,

and our RAM ZK data structures from VOLE in C++. We use

the learning-parity-with-noise-based VOLE protocol of [44]

which is implemented as part of the EMP Toolkit [43]. While

our VOLE-based approach will extend to any large ﬁeld, we

use the ﬁeld

−1

because this is the only arithmetic ﬁeld

currently implemented by EMP.

[26] and [20] implementation. We compare our RAM to

that of [26] and of [20]. We also compare our ROM to that of

[26]. [26]’s RAM/ROM implementation is publicly available

as part of the EMP Toolkit [43]. [20]’s RAM implementation

is not publicly available. We implemented a VOLE-based

version of their RAM

in C++. Other ZK RAMs do not have

constant overhead per access.

As discussed in Section 3, [20]’s RAM leverages permu-

tation proofs. Recall, VOLE-based ZK offer optimizations

for permutation proofs (see Section 5.2). We also note that

several gates in [20]’s protocol can be further optimized in

VOLE-based ZK. In particular, these gates require checking

that the product of two wires is some constant; such checks

can be done in VOLE-based ZK without communication. For

fair comparison, we incorporate all such VOLE-based opti-

mizations in our implementation of [20].

Experimental setup. We ran all three RAMs on a bench-

mark where we instantiate a RAM of sizes

ranging from

and perform

T = 2

accesses. We run our ROM, [26]’s

ROM, and our set data structure with the same n and T .

In all cases,

and

run single threaded on a separate

Amazon EC2

m5.2xlarge

machine

. We measure total (and

per-access) communication in bytes and per-access runtime

in microseconds. For the latter, we experiment with different

network bandwidth settings, varying between a WAN-like

25Mbps connection and a LAN-like 1Gbps connection.

Parameter

for accelerating permutation proofs. Our

RAM, ROM, and set data structures (and our imple-

mented [20]’s RAM) all beneﬁt from VOLE-based polyno-

mial proofs used to optimize to high-fan-in multiplications

(see Section 5.2). In particular, recall that parameter

trades

off between number of required VOLE correlations and

computation. Figure 10 tabulates the impact of

on perfor-

mance (we set n = 2

and T = 2

For simplicity of implementation, we organize our high fan-

in-

multiplications as trees of multiplications, and we only

use fan-in-

gates at the widest tree level. The remaining mul-

tiplications are achieved with fan-in-two gates. This means

our high fan-in gates use

≈

VOLES, rather than

⌈

ε−1

⌉

In practice, the change in performance is not noticeable.

[20]’s RAM was designed for the MPC-in-the-head paradigm, but, like

our RAM, it is a pure arithmetic circuit with random challenges, so it can

also be implemented for VOLE-ZK.

[26] reported clear concrete improvements over earlier ZK RAMs.

Intel Xeon Platinum 8175 CPU @ 3.10GHz,

vCPUs,

GiB Memory,

10Gbps Network

n = 2

Bandwidth

2 4 8 16 32 64 128

Set

25 Mbps 8.88 6.14 4.78 4.10 3.62 3.62 3.87

100 Mbps 2.39 1.72 1.41 1.21 1.14 1.29 1.54

500 Mbps 0.80 0.69 0.63 0.65 0.64 0.77 1.04

1 Gbps 0.66 0.60 0.59 0.61 0.61 0.73 1.01

Comm. (byte) 27.1 18.6 14.4 12.2 10.9 10.3 10.1

ROM

25 Mbps 12.56 9.66 8.21 7.49 7.17 7.18 7.46

100 Mbps 3.37 2.64 2.28 2.09 2.14 2.24 2.58

500 Mbps 1.10 0.96 0.93 0.95 1.02 1.17 1.47

1 Gbps 0.92 0.85 0.83 0.85 0.94 1.06 1.38

Comm. (byte) 38.4 29.4 24.9 22.7 21.6 21.0 20.7

RAM

25 Mbps 28.92 21.73 18.38 16.55 15.58 15.59 16.26

100 Mbps 7.80 5.94 5.15 4.53 4.58 4.91 5.60

500 Mbps 2.60 2.01 1.96 1.93 1.99 2.33 3.03

1 Gbps 2.14 1.74 1.72 1.67 1.78 2.11 2.87

Comm. (byte) 88.3 66.4 55.9 50.3 47.4 46.1 45.4

Figure 10: Per-access runtime (

µs

) and communication

(bytes) of our data structures as a function of

, the degree of

polynomials used in our handling of high fan-in multiplica-

tions; see Section 5.2. As

increases, we use fewer VOLE

correlations, but P computes more ﬁeld operations.

11 12 13 14 15 16 17 18 19 20

Time

logn

25 Mbps

100 Mbps

500 Mbps

1 Gbps

Figure 11: Per-access runtime of our RAM (µs).

In subsequent experiments, we set

ε = 16

. Increasing

beyond this point yields greatly diminished communication

improvement, as input gates dominate cost and are not im-

proved by increasing ε.

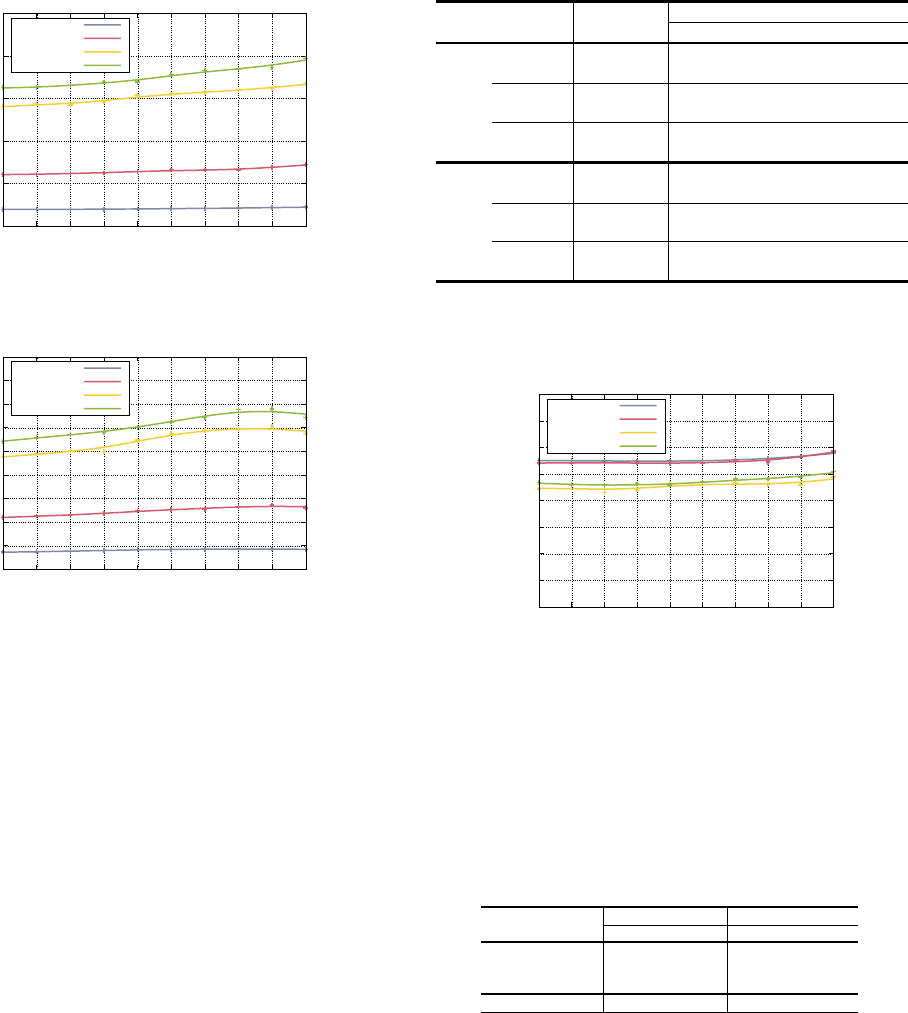
Our RAM performance. Figure 11 plots per-access run-

time of our RAM in microseconds. On a slow

Mbps WAN-

like connection, our RAM requires

∼ 15µs

per access; On

a faster

100

Mbps WAN-like connection, our RAM requires

< 5µs

per access; On a

Gbps LAN-like connection, our

RAM requires only

∼ 1.5µs

per access, achieving access at

≈ 600

KHz. As

ranges from

, the per-access

communication increases only from

bytes; runtime

remains essentially unchanged (caching begins to impact per-

formance at high n). The full version includes detailed data.

Our ROM and set performance. On a

Mbps WAN-like

connection, our ROM (resp. set) requires

< 8µs

(resp.

< 4µs

)

per access; on a

Gbps LAN-like connection, our ROM (resp.

set) requires

∼ 1µs

(resp.

< 1µs

) per access. As

ranges

11 12 13 14 15 16 17 18 19 20

Speedup over [26]

logn

25 Mbps

100 Mbps

500 Mbps

1 Gbps

Figure 12: Speedup of our RAM over [26]’s RAM.

11 12 13 14 15 16 17 18 19 20

Speedup over [26]

logn

25 Mbps

100 Mbps

500 Mbps

1 Gbps

Figure 13: Our ROM’s speedup over [26]’s ROM.

from

, the per-access communication is

19-22

(resp.

10-12

) bytes; runtime remains essentially unchanged (caching

effects begin to impact performance at high

). We defer plots

and detailed data to the full version.

Our RAM/ROM vs. [26]’s RAM/ROM. Figures 12 and 13

plot our RAM/ROM’s speedup over [26]’s RAM/ROM.

Speedup is deﬁned by per-access

baseline

ours

. [26]’s imple-

mentation is over Boolean circuits with

ring algebraic

structure. Our ROM improves over [26]’s ROM by

3-34×

depending on bandwidth. Our RAM improves over [26]’s

RAM by

2-20×

. Figure 14 tabulates communication required

by our RAM/ROM as compared to [26].

Our speedup comes primarily from improved computation,

resulting from a greatly reduced number of gates. Note the

signiﬁcant communication reduction from

, reﬂecting

our reduction in the number of required VOLE correlations.

Our RAM vs. [20]’s RAM. Figure 15 plots our RAM

speedup over our optimized implementation of [20]’s RAM.

Even though we heavily optimize [20]’s RAM, our RAM

still improves per-access runtime by

2.2-2.9×

. As

ranges

from

, [20]’s per-access communication goes from

129 to 145 bytes, which is ≈ 3× more than our RAM.

Direction Benchmark

logn

12 14 16 18 20

ROM

P → V

[26] 28.4 29.2 30.1 31.5 34.7

Ours 18.4 18.5 18.6 19.2 21.8

V → P

[26] 12.6 12.9 13.4 14.0 15.3

Ours 0.7 0.7 0.7 0.7 0.9

Total

[26] 41.0 42.1 43.5 45.6 50.1

Ours 19.1 19.2 19.3 19.9 22.7

RAM

P → V

[26] 32.3 33.1 34.1 35.5 39.2

Ours 45.7 45.8 45.9 46.5 49.0

V → P

[26] 14.5 14.8 15.2 15.9 17.5

Ours 1.3 1.3 1.3 1.3 1.3

Total

[26] 46.9 48.0 49.3 51.4 56.8

Ours 47.1 47.1 47.3 47.9 50.3

Figure 14: Per-access communication (bytes) used by our

ROM (resp. RAM) versus [26]’s ROM (resp. RAM).

0.5

1.5

2.5

3.5

11 12 13 14 15 16 17 18 19 20

Speedup over [20]

logn

25 Mbps

100 Mbps

500 Mbps

1 Gbps

Figure 15: Our RAM’s speedup over [20]’s RAM (we opti-

mize [20]’s RAM).

As one additional data-point, we disabled all VOLE-based

optimizations for both our RAM and our implementation of

[20], then ran with

n = 2

. Here, our RAM requires

bytes

per access while [20] requires

242

bytes. These numbers

reﬂect our raw advantage in total number of non-linear gates.

n = 2

ROM RAM

Bandwidth (Mbps) 25 100 500 25 100 500

Setup 0.66 0.26 0.19 0.76 0.38 0.32

Access 5.30 1.38 0.47 10.56 2.73 0.87

Teardown 1.53 0.45 0.29 5.23 1.42 0.74

Total 7.49 2.09 0.95 16.55 4.53 1.93

Figure 16: Runtime cost breakdown of our ROM/RAM (

µs

Microbenchmarks. Figure 16 breaks down the per-access

runtime of our RAM and ROM. The main components include

setup, access, and teardown (see Figures 7 and 9). Access

clearly dominates cost, and setup is by far the cheapest step.

Acknowledgements

This research was developed with the support of funding under

NSF grants CNS-2246353 and CNS-2246354.

References

[1]

Scott Ames, Carmit Hazay, Yuval Ishai, and Muthura-

makrishnan Venkitasubramaniam. Ligero: Lightweight

sublinear arguments without a trusted setup. In Proceed-

ings of the 2017 acm sigsac conference on computer

and communications security, pages 2087–2104, 2017.

[2]

Diego F Aranha, Emil Madsen Bennedsen, Matteo Cam-

panelli, Chaya Ganesh, Claudio Orlandi, and Akira

Takahashi. Eclipse: enhanced compiling method for

pedersen-committed zksnark engines. In Public-Key

Cryptography–PKC 2022: 25th IACR International Con-

ference on Practice and Theory of Public-Key Cryptog-

raphy, Virtual Event, March 8–11, 2022, Proceedings,

Part I, pages 584–614. Springer, 2022.

[3]

Carsten Baum, Lennart Braun, Alexander Munch-

Hansen, Benoit Razet, and Peter Scholl. Appenzeller to

brie: efﬁcient zero-knowledge proofs for mixed-mode

arithmetic and

. In Proceedings of the 2021 ACM

SIGSAC Conference on Computer and Communications

Security, pages 192–211, 2021.

[4]

Carsten Baum, Lennart Braun, Alexander Munch-

Hansen, and Peter Scholl. Moz

arella: efﬁcient vector-

ole and zero-knowledge proofs over

. In Advances in

Cryptology–CRYPTO 2022: 42nd Annual International

Cryptology Conference, CRYPTO 2022, Santa Barbara,

CA, USA, August 15–18, 2022, Proceedings, Part IV,

pages 329–358. Springer, 2022.

[5]

Carsten Baum, Alex J Malozemoff, Marc B Rosen, and

Peter Scholl. Mac’n’cheese: Zero-knowledge proofs for

boolean and arithmetic circuits with nested disjunctions.

In Advances in Cryptology–CRYPTO 2021: 41st Annual

International Cryptology Conference, CRYPTO 2021,

Virtual Event, August 16–20, 2021, Proceedings, Part

IV 41, pages 92–122. Springer, 2021.

[6]

Eli Ben-Sasson, Alessandro Chiesa, Daniel Genkin,

Eran Tromer, and Madars Virza. SNARKs for C: Veri-

fying program executions succinctly and in zero knowl-

edge. In Ran Canetti and Juan A. Garay, editors,

CRYPTO 2013, Part II, volume 8043 of LNCS, pages

90–108. Springer, Heidelberg, August 2013.

[7]

Eli Ben-Sasson, Alessandro Chiesa, Daniel Genkin,

Eran Tromer, and Madars Virza. Snarks for c: Verifying

program executions succinctly and in zero knowledge.

In Advances in Cryptology–CRYPTO 2013: 33rd An-

nual Cryptology Conference, Santa Barbara, CA, USA,

August 18-22, 2013. Proceedings, Part II, pages 90–108.

Springer, 2013.

[8]

Eli Ben-Sasson, Alessandro Chiesa, Eran Tromer, and

Madars Virza. Succinct non-interactive zero knowledge

for a von neumann architecture. In 23rd USENIX Secu-

rity Symposium (USENIX Security 14), pages 781–796,

2014.

[9]

Václav E Beneš. Permutation groups, complexes, and re-

arrangeable connecting networks. Bell System Technical

Journal, 43(4):1619–1640, 1964.

[10]

Alexander R Block, Justin Holmgren, Alon Rosen,

Ron D Rothblum, and Pratik Soni. Public-coin zero-

knowledge arguments with (almost) minimal time and

space overheads. In Theory of Cryptography: 18th In-

ternational Conference, TCC 2020, Durham, NC, USA,

November 16–19, 2020, Proceedings, Part II, pages 168–

197. Springer, 2020.

[11]

Alexander R Block, Justin Holmgren, Alon Rosen,

Ron D Rothblum, and Pratik Soni. Time-and space-

efﬁcient arguments from groups of unknown order. In

Advances in Cryptology–CRYPTO 2021: 41st Annual

International Cryptology Conference, CRYPTO 2021,

Virtual Event, August 16–20, 2021, Proceedings, Part

IV 41, pages 123–152. Springer, 2021.

[12]

Manuel Blum, Will Evans, Peter Gemmell, Sampath

Kannan, and Moni Naor. Checking the correctness of

memories. Algorithmica, 12:225–244, 1994.

[13]

Jonathan Bootle, Andrea Cerulli, Jens Groth, Sune

Jakobsen, and Mary Maller. Arya: Nearly linear-time

zero-knowledge proofs for correct program execution.

In Advances in Cryptology–ASIACRYPT 2018: 24th

International Conference on the Theory and Applica-

tion of Cryptology and Information Security, Brisbane,

QLD, Australia, December 2–6, 2018, Proceedings, Part

I, pages 595–626. Springer, 2018.

[14]

Benjamin Braun, Ariel J Feldman, Zuocheng Ren, Sri-

nath Setty, Andrew J Blumberg, and Michael Walﬁsh.

Verifying computations with state. In Proceedings of the

twenty-fourth ACM Symposium on Operating Systems

Principles, pages 341–357, 2013.

[15]

Benedikt Bünz, Jonathan Bootle, Dan Boneh, Andrew

Poelstra, Pieter Wuille, and Greg Maxwell. Bulletproofs:

Short proofs for conﬁdential transactions and more. In

2018 IEEE Symposium on Security and Privacy, pages

315–334. IEEE Computer Society Press, May 2018.

[16]

Ran Canetti. Universally composable security: A new

paradigm for cryptographic protocols. In Proceedings

42nd IEEE Symposium on Foundations of Computer

Science, pages 136–145. IEEE, 2001.

[17]

Ran Canetti, Yehuda Lindell, Rafail Ostrovsky, and Amit

Sahai. Universally composable two-party and multi-

party secure computation. In Proceedings of the Thiry-

Fourth Annual ACM Symposium on Theory of Comput-

ing, STOC ’02, page 494–503, New York, NY, USA,

2002. Association for Computing Machinery.

[18]

Alessandro Chiesa, Yuncong Hu, Mary Maller, Pratyush

Mishra, Noah Vesely, and Nicholas P. Ward. Marlin:

Preprocessing zkSNARKs with universal and updatable

SRS. In Anne Canteaut and Yuval Ishai, editors, EU-

ROCRYPT 2020, Part I, volume 12105 of LNCS, pages

738–768. Springer, Heidelberg, May 2020.

[19]

Cyprien de Saint Guilhem, Emmanuela Orsini, and

Titouan Tanguy. Limbo: Efﬁcient zero-knowledge

MPCitH-based arguments. In Giovanni Vigna and

Elaine Shi, editors, ACM CCS 2021, pages 3022–3036.

ACM Press, November 2021.

[20]

Cyprien Delpech de Saint Guilhem, Emmanuela Orsini,

Titouan Tanguy, and Michiel Verbauwhede. Efﬁcient

proof of ram programs from any public-coin zero-

knowledge system. In Clemente Galdi and Stanis-

law Jarecki, editors, Security and Cryptography for Net-

works, pages 615–638, Cham, 2022. Springer Interna-

tional Publishing.

[21]

Richard A. DeMillo and Richard J. Lipton. A probabilis-

tic remark on algebraic program testing. Information

Processing Letters, 7(4):193–195, 1978.

[22]

Samuel Dittmer, Yuval Ishai, Steve Lu, and Rafail Os-

trovsky. Improving line-point zero knowledge: Two

multiplications for the price of one. In Proceedings of

the 2022 ACM SIGSAC Conference on Computer and

Communications Security, pages 829–841, 2022.

[23]

Samuel Dittmer, Yuval Ishai, and Rafail Ostrovsky. Line-

Point Zero Knowledge and Its Applications. In Ste-

fano Tessaro, editor, 2nd Conference on Information-

Theoretic Cryptography (ITC 2021), volume 199 of Leib-

niz International Proceedings in Informatics (LIPIcs),

pages 5:1–5:24, Dagstuhl, Germany, 2021. Schloss

Dagstuhl – Leibniz-Zentrum für Informatik.

[24]

Cynthia Dwork, Moni Naor, Guy N. Rothblum, and

Vinod Vaikuntanathan. How efﬁcient can memory

checking be? In Omer Reingold, editor, TCC 2009,

volume 5444 of LNCS, pages 503–520. Springer, Hei-

delberg, March 2009.

[25]

Zhiyong Fang, David Darais, Joseph P. Near, and Yu-

peng Zhang. Zero knowledge static program analysis.

In Giovanni Vigna and Elaine Shi, editors, ACM CCS

2021, pages 2951–2967. ACM Press, November 2021.

[26]

Nicholas Franzese, Jonathan Katz, Steve Lu, Rafail Os-

trovsky, Xiao Wang, and Chenkai Weng. Constant-

overhead zero-knowledge for RAM programs. In Gio-

vanni Vigna and Elaine Shi, editors, ACM CCS 2021,

pages 178–191. ACM Press, November 2021.

[27]

Ariel Gabizon and Zachary J. Williamson. plookup: A

simpliﬁed polynomial protocol for lookup tables. Cryp-

tology ePrint Archive, Report 2020/315, 2020.

https:

//eprint.iacr.org/2020/315.

[28]

S Goldwasser, S Micali, and C Rackoff. The knowledge

complexity of interactive proof-systems. In Proceedings

of the Seventeenth Annual ACM Symposium on Theory

of Computing, STOC ’85, page 291–304, New York, NY,

USA, 1985. Association for Computing Machinery.

[29]

Paul Grubbs, Arasu Arun, Ye Zhang, Joseph Bonneau,

and Michael Walﬁsh.

{

Zero-Knowledge

}

middleboxes.

In 31st USENIX Security Symposium (USENIX Security

22), pages 4255–4272, 2022.

[30]

David Heath and Vladimir Kolesnikov. A 2.1 KHz zero-

knowledge processor with BubbleRAM. In Jay Ligatti,

Xinming Ou, Jonathan Katz, and Giovanni Vigna, ed-

itors, ACM CCS 2020, pages 2055–2074. ACM Press,

November 2020.

[31]

David Heath and Vladimir Kolesnikov. PrORAM -

fast

O(logn)

authenticated shares ZK ORAM. In

Mehdi Tibouchi and Huaxiong Wang, editors, ASI-

ACRYPT 2021, Part IV, volume 13093 of LNCS, pages

495–525. Springer, Heidelberg, December 2021.

[32]

David Heath, Yibin Yang, David Devecsery, and

Vladimir Kolesnikov. Zero knowledge for everything

and everyone: Fast zk processor with cached oram for

ansi c programs. In 2021 IEEE Symposium on Security

and Privacy (SP), pages 1538–1556. IEEE, 2021.

[33] Zhangxiang Hu, Payman Mohassel, and Mike Rosulek.

Efﬁcient zero-knowledge proofs of non-algebraic state-

ments with sublinear amortized cost. In Advances in

Cryptology–CRYPTO 2015: 35th Annual Cryptology

Conference, Santa Barbara, CA, USA, August 16-20,

2015, Proceedings, Part II 35, pages 150–169. Springer,

2015.

[34]

Yuval Ishai, Eyal Kushilevitz, Rafail Ostrovsky, and

Amit Sahai. Zero-knowledge from secure multiparty

computation. In Proceedings of the Thirty-Ninth Annual

ACM Symposium on Theory of Computing, STOC ’07,

page 21–30, New York, NY, USA, 2007. Association

for Computing Machinery.

[35]

Ning Luo, Timos Antonopoulos, William R. Harris, Ruz-

ica Piskac, Eran Tromer, and Xiao Wang. Proving UN-

SAT in zero knowledge. In Heng Yin, Angelos Stavrou,

Cas Cremers, and Elaine Shi, editors, ACM CCS 2022,

pages 2203–2217. ACM Press, November 2022.

[36]

Mary Maller, Sean Bowe, Markulf Kohlweiss, and Sarah

Meiklejohn. Sonic: Zero-knowledge SNARKs from

linear-size universal and updatable structured reference

strings. In Lorenzo Cavallaro, Johannes Kinder, Xi-

aoFeng Wang, and Jonathan Katz, editors, ACM CCS

2019, pages 2111–2128. ACM Press, November 2019.

[37]

Payman Mohassel, Mike Rosulek, and Alessandra Sca-

furo. Sublinear zero-knowledge arguments for ram

programs. In Advances in Cryptology–EUROCRYPT

2017: 36th Annual International Conference on the

Theory and Applications of Cryptographic Techniques,

Paris, France, April 30–May 4, 2017, Proceedings, Part

I, pages 501–531. Springer, 2017.

[38]

C. Andrew Neff. A veriﬁable secret shufﬂe and its

application to e-voting. In Michael K. Reiter and

Pierangela Samarati, editors, ACM CCS 2001, pages

116–125. ACM Press, November 2001.

[39]

Eli Ben Sasson, Alessandro Chiesa, Christina Garman,

Matthew Green, Ian Miers, Eran Tromer, and Madars

Virza. Zerocash: Decentralized anonymous payments

from bitcoin. In 2014 IEEE symposium on security and

privacy, pages 459–474. IEEE, 2014.

[40]

J. T. Schwartz. Fast probabilistic algorithms for veriﬁ-

cation of polynomial identities. J. ACM, 27(4):701–717,

oct 1980.

[41]

Riad S. Wahby, Srinath Setty, Zuocheng (Andy) Ren,

Andrew J. Blumberg, and Michael Walﬁsh. Efﬁcient

RAM and control ﬂow in veriﬁable outsourced compu-

tation. In NDSS, 2015.

[42]

Abraham Waksman. A permutation network. J. ACM,

15(1):159–163, January 1968.

[43]

Xiao Wang, Alex J. Malozemoff, and Jonathan Katz.

EMP-toolkit: Efﬁcient MultiParty computation toolkit.

https://github.com/emp-toolkit, 2016.

[44]

Chenkai Weng, Kang Yang, Jonathan Katz, and Xiao

Wang. Wolverine: fast, scalable, and communication-

efﬁcient zero-knowledge proofs for boolean and arith-

metic circuits. In 2021 IEEE Symposium on Security

and Privacy (SP), pages 1074–1091. IEEE, 2021.

[45]

Chenkai Weng, Kang Yang, Xiang Xie, Jonathan Katz,

and Xiao Wang. Mystique: Efﬁcient conversions for

zero-knowledge proofs with applications to machine

learning. In USENIX Security Symposium, pages 501–

518, 2021.

[46]

Chenkai Weng, Kang Yang, Zhaomin Yang, Xiang Xie,

and Xiao Wang. Antman: Interactive zero-knowledge

proofs with sublinear communication. In Proceedings

of the 2022 ACM SIGSAC Conference on Computer and

Communications Security, pages 2901–2914, 2022.

[47]

Kang Yang, Pratik Sarkar, Chenkai Weng, and Xiao

Wang. Quicksilver: Efﬁcient and affordable zero-

knowledge proofs for circuits and polynomials over any

ﬁeld. In Proceedings of the 2021 ACM SIGSAC Confer-

ence on Computer and Communications Security, pages

2986–3001, 2021.

[48]

Yibin Yang and David Heath. Two shufﬂes make a

ram: Improved constant overhead zero knowledge ram.

Cryptology ePrint Archive, 2023.

https://eprint.

iacr.org/2023/1115.

[49]

Yibin Yang, David Heath, Vladimir Kolesnikov, and

David Devecsery. Ezee: Epoch parallel zero knowl-

edge for ansi c. In 2022 IEEE 7th European Symposium

on Security and Privacy (EuroS&P), pages 109–123.

IEEE, 2022.

[50]

Yupeng Zhang, Daniel Genkin, Jonathan Katz, Dimitrios

Papadopoulos, and Charalampos Papamanthou. vRAM:

Faster veriﬁable RAM with program-independent pre-

processing. In 2018 IEEE Symposium on Security and

Privacy, pages 908–925. IEEE Computer Society Press,

May 2018.

[51]

Richard Zippel. An explicit separation of relativised ran-

dom polynomial time and relativised deterministic poly-

nomial time. Information Processing Letters, 33(4):207–

212, 1989.

Appendix A Commit-and-Prove ZK

For completeness, Figure 17 lists the standard commit-and-

prove ZK functionality, as formalized by [17].

Functionality F

considers a prover

, a veriﬁer

, and an adversary

S, and it is parameterized by a ﬁeld F:

Commits: Upon receiving

(commit,cid,x)

from

where

(a) there is no recorded tuple

(cid,·)

, and (b)

x ∈ F

: Record

the tuple (cid,x) and send (commit, cid) to S and V .

Proof: Upon receiving

(prove,C,cid

,...,cid

)

from

where (1)

is a circuit

C : F

(n)

7→ F

, and (b) each

cid

i∈[n]

was recorded:

•

Fetch recorded

(cid

),...,(cid

)

, compute

y :=

C(x

,...,x

)

. If

y = 0

, send

(prove,C,cid,true)

and V ; else send (prove,C,cid,false) to S and V .

Figure 17: The commit-and-prove ZK functionality.

Appendix B Proof of Security

B.1 Soundness Lemmas

Protocol 1 requires that

input extra ﬁeld elements. The

soundness of our protocol is based on the fact that even a ma-

licious

cannot input values that disagree with the semantics

of ROM/RAM. This section formalizes

’s inability to cheat

as security games and lemmas. Our main proof of security

relies on these lemmas.

Lemma 2. Let

be a prime ﬁeld, and let

a positive integer

s.t.

m < |F|

. Let

P ≜ {t

,...,t

}

be an ordered set of any

ﬁeld elements. Let

Q ≜ {t

+ 1,...,t

+ 1}

be an ordered set.

P and Q cannot form a permutation: P ̸∼ Q.

Proof.

By induction on the entries of

and

. Consider

. By construction, we ensure

+ 1

is in

. If

P ∼ Q

then

+ 1

is also in

. By repeating this argument,

must

have

+1,t

+2, . ..,t

+m −1

. Accordingly,

must have

+1,t

+2,t

+3, . ..,t

. However, since

m < |F|

/∈ Q

contradicting P ∼ Q.

Game 1 (Single Element ROM). Let

be a prime ﬁeld, and

let

T ∈ N

s.t.

T < |F|

. Consider lists

and

, both initialized

as empty. Let

begin

∈ F

be arbitrary values. The

round game with A proceeds as follows:

1. Append (c

begin

) to W.

In each round

i ∈ [T ]

chooses

∈ F

. Append

)

to R; append (c

+ 1) to W.

After

rounds:

chooses

end

∈ F

. Append

end

) to R.

We say that A wins i.f.f. W ∼ R at the end of the game.

Lemma 3. If A wins Game 1, then the following must hold:

begin

= c

= ··· = c

= c

end

Namely, each

i∈[T ]

and

end

provided by

are equal to

begin

Proof. By induction on T .

Base case: When

T = 0

(resp.

) only has a sin-

gle element

begin

)

(resp.

end

)

). If

W ∼ R

, then

the single element in

must be

begin

)

. This implies

begin

= c

end

, so the lemma holds.

Induction: By the inductive hypothesis, the lemma holds

when

T = n

. Consider

T = n + 1

. Suppose

wins the game

when

T = n + 1

, and thus

R ∼ W

. Consider

begin

)

. The value

begin

)

must be in

, and there are two

possible placements of this value:

1. (c

begin

) is the last element of R:

end

) = (c

begin

)

If we ignore

end

)

and

begin

)

, then

the remaining

n + 1

elements in

and

must still form

a permutation:

{(c

),...,(c

)} ∼ {(c

+ 1),...,(c

+ 1)}

But this is impossible by Lemma 2.

2. (c

begin

)

is not the last element of

. I.e., there exists

some j ∈ [n + 1] such that:

) = (c

begin

)

In this case, the corresponding tuple appended to

in round

j (c

+ 1)

can be understood as a tuple

′

begin

′

begin

)

in a new game with

′

= T − 1 = n

. By

the inductive hypothesis, we know all

i̸= j

and

end

are

equal to

, and

is equal to

begin

. Thus, the lemma

holds for T = n + 1.

Note, the inductive argument only holds when T < |F|.

Game 2 (ROM). Let

be a prime ﬁeld, and let

n,T ∈ N

s.t.

n,T < |F|. Consider lists R and W, both initialized as empty.

Consider a size-

set of ﬁeld elements

{ℓ

,...,ℓ

}

called the

address set. For each

ℓ

k∈[n]

, let

k,begin

∈ F

be arbitrary

values. The T-round game with A proceeds as follows:

1. For each k ∈ [n], append (ℓ

k,begin

) to W.

In each round

i ∈ [T ]

chooses

∈ F

and

∈ [n]

Append (ℓ

) to R; append (ℓ

+ 1) to W.

After

rounds: for each

ℓ

k∈[n]

chooses

k,end

∈

F. Append (ℓ

k,end

) to R.

We say that A wins i.f.f. W ∼ R at the end of the game.

Lemma 4. If A wins Game 2, then the following must hold:

∀k ∈ [n], ∀(ℓ

,c,t) ∈ R,c = c

k,begin

Namely, once

selects

in each round,

must be equal to

,begin

. Also, c

k,end

= c

k,begin

for each k ∈ [n].

Proof.

By partitioning

and

into address-speciﬁc permu-

tations, then applying Lemma 3.

In more detail, recall that in each round

i ∈ [T ]

selects

∈ [n]

. We denote by

the number of rounds where

selects

= k

. For each

k ∈ [n]

, we deﬁne address-speciﬁc

reads and writes:

≜ {(c,t) | (ℓ

,c,t) ∈ W}

≜ {(c,t) | (ℓ

,c,t) ∈ R}

Note,

| = |R

| = T

+ 1

. Since

W ∼ R

, and since each

tuple is explicitly tagged with its address

ℓ

, it must be that

∼ R

. For each

, we can now apply a

-round Game 1

and

, where

begin

)

is set to

k,begin

)

Since

≤ T < |F|

, applying Lemma 3

times completes the

proof.

Game 3 (Single Element RAM). Let

be a prime ﬁeld, and

let

T ∈ N

s.t.

T > 1

and

|F| ≥ 2T

. Consider lists

and

both initialized as empty. Let

begin

∈ F

be an arbitrary value.

Consider a non-empty size-

set

S ≜ {s

,...,s

}

called the

timestamp set where:

1 ≤ s

< s

< ··· < s

≤ T

The m-round game with A proceeds as follows:

1. Append (c

begin

,0) to W.

For each round

i ∈ [m]

chooses

∈ F

. Ap-

pend

)

; append

,embed(s

))

where

embed(·)

denotes the trivial embedding from

[T ]

(henceforth, we omit calls to embed).

After

rounds:

chooses

end

∈ F

. Append

end

) to R.

We say that A wins i.f.f. at the end of the game:

W ∼ R and ∀i ∈ [m],(s

−t

) ∈ {1,2,...,T }

Lemma 5. If A wins Game 3, it must be that W = R.

Proof.

In short, we argue that at each round

has exactly

one value it can “read” (similar to Invariant 2).

In more detail, note:

W = {(c

begin

,0),(c

),...,(c

)}

If W ∼ R, then it must be that the following holds:

,...,t

end

} ∼ {0,s

,...,s

} (1)

Consider

. By Equation (1), we know

∈ {0,s

,...,s

}

and because

won the game, we know

−t

) ∈ {1,...,T }

Now, we argue it must be that

= 0

. Indeed, any other choice

∈ {s

,...,s

}

will yield a difference

−t

that outside the

allowed range

{1,...,T }

. This is because

− s

, and all

other choices s

are even greater than s

− s

+ |F| ≥ 1 − T + |F| > T

Similarly, consider

. By Equation (1), we know

∈

{0,s

,...,s

}

, and because

won the game, we know

−t

) ∈ {1,...,T }. It must be that t

= s

. Indeed:

− s

+ |F| ≥ 1 − T + |F| > T

Thus,

must be in the set

{0,s

}

. Moreover,

= 0

, so to

satisfy the permutation requirement, t

can only be s

We can inductively repeat the above analysis for each

∗

I.e., t

= s

i−1

(assume s

= 0) for all i ∈ [m] and t

end

= s

To sum up,

,...,t

end

} = {0,s

,...,s

}

, where we in-

terpret these as ordered sets. Note that each

is distinct and

non-zero. Since W ∼ R, it must be that W = R.

Game 4 (RAM). Let

be a prime ﬁeld, and let

T ∈ N

s.t.

T >

and

|F| > 2T − 1

. Consider lists

and

, both initialized

as empty. Consider a set of ﬁeld elements {ℓ

,...,ℓ

} called

the address set. For each

ℓ

k∈[n]

, let

k,begin

∈ F

be an arbitrary

ﬁeld element. The

-round game with

proceeds as follows:

1. For each k ∈ [n], append (ℓ

k,begin

,0) to W.

For each round

i ∈ [T ]

chooses

∈ F

and

∈

[n]. Append (ℓ

) to R; append (ℓ

,i) to W.

After

rounds: for each

ℓ

k∈[n]

chooses

k,end

∈

F. Append (ℓ

k,end

) to R.

We say that A wins i.f.f. at the end of the game:

W ∼ R and ∀i ∈ [T ],(i −t

) ∈ {1,2,...,T }

Lemma 6. If

wins Game 4, then the following must hold:

For each k ∈ [n], deﬁne lists W

and R

as follows:

≜ {(c,t) | (ℓ

,c,t) ∈ W}

≜ {(d,t) | (ℓ

,d,t) ∈ R}

I.e., fetch (in order) the tuples in

and

with

ℓ

as the

address. For each k, it holds that W

= R

Proof.

Immediate, by partitioning

and

into address-

speciﬁc permutations, then applying Lemma 5 n times.

B.2 Proof of Lemma 1

We instantiate our protocols as a VOLE-based ZK system.

Lemma 1 shows that

perm

can be UC-realized in the VOLE-

hybrid model. This is achieved by prior work, e.g., [26,47].

For completeness, we state facts supported by prior work.

Lemma 7. There exists a

-round protocol in the VOLE-

hybrid model that UC-realizes

perm

without permutation

gates. For each use of

input

and of

and

use

VOLE correlation. The protocol achieves soundness error

|F|

), where m is the number of multiplications.

Proof. See [47].

Lemma 8. There exists a

-round protocol in the VOLE-

hybrid model that UC-realizes

perm

with only permutation

and input gates. For each use of

input

and

use

VOLE

correlation; for each use of

∼

on two length-

vectors,

and

each evaluate

O(n)

ﬁeld operations and consume

ε−1

+ o(1)

VOLE correlations, for any constant

ε ≥ 2

. The

protocol achieves soundness error

|F|

)

, where

is the size

of the largest vector passed to ∼ .

Proof. See [26].

The proof of Theorem 1 is included in the full version.

This does not imply that W and R will be identical.